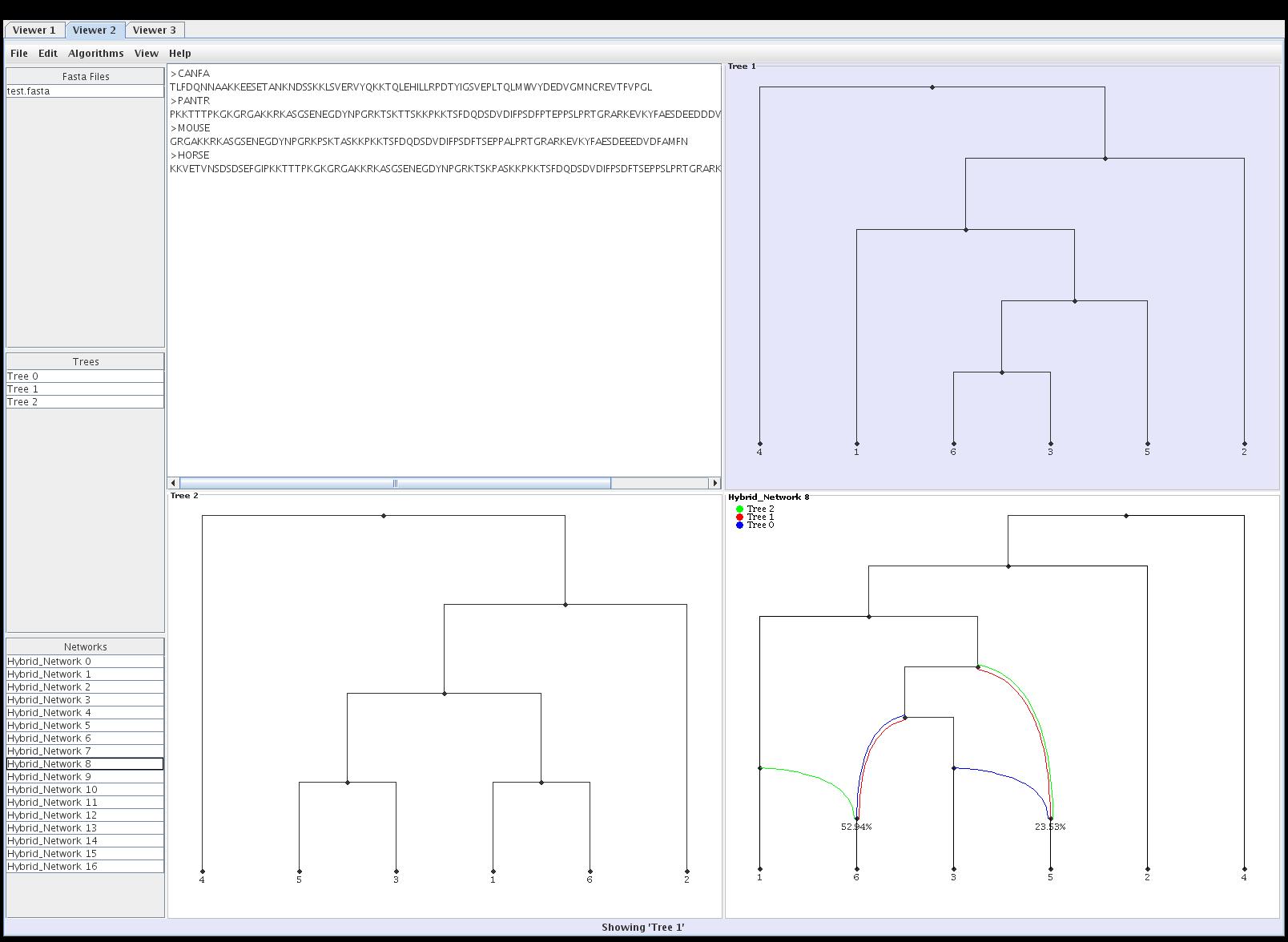
Hybroscale
There exist some programs for visualizing rooted trees or networks, only
few programs for both computing and studying hybridization networks
displaying two bifurcating input trees, and no program, however,
computing all hybridization networks for an arbitrary number (>2) of
non-binary input trees sharing just an overlapping set of
taxa. Hybroscale is specifically designed to combine all of those
functionalities that are, obviously, of high interest for the research
of retiuculate evolution. This program contains a graphical user
interface, which enables an easy handling of its algorithms and
visualization methods.
Download
The program is offered as runnable jar file requiring Java 1.7 or
higher. For a detailed description of how to use the program please have
a look at the manual.
Latest Changes
Performance improved by working on bottlenecks in terms of
time and space comsumption. Redundancy of underlying algorithms
reduced. Method for re-rooting trees by hybridization number
added. New design and new features ensuring a better
useability.
Constraints added for pruning network search spaces or for
filtering a set of calculated networks. The work is motivated
by the paper "Fighting network space: it is time for an
SQL-type language to filter phylogenetic networks"
(arXiv:1310.6844).
Modification to our algorithm such that now all networks
for multiple multifurcating trees sharing just an overlapping
set of taxa can be computed.
Contact
If you have any questions or suggestions how to improve Hybroscale,
please contact
Benjamin
Albrecht .
Simulation
To show the efficiency of its algorithm computing all hybridization
networks for multiple input trees, we have generated a synthetic dataset
and performed a simulation study comparing Hybroscale against PIRN
v.2.0.1 which is, to our knowledge, the best available software for
computing hybridization numbers for more than two input trees. The
synthetic dataset contains tree sets of four different parameters,
namely the number of input trees n, the number of leaves l, an upper
bound for the hybridization number k, and the tangling degree t. Each
input tree of a tree set of size n is an embedded tree of a certain
bicombining network that is computed in respect to these five different
parameters as follows: Firstly, a random binary tree containing l leaves
is computed and, secondly, k edges are inserted in respect to the
parameter t such that the resulting network contains k reticulation
nodes with indegree two.
Both software packages have been run on a grid computer containing 16
cores and 40GB RAM for our synthetic dataset consisting of 2430 tree
sets with parameters n in {3,4,5}, l in {10,25,50}, k in {5,10,15}, and
t in {1,3,5}. The result of our simulation study as well as the
synthetic dataset can be downloaded from below:
Publications
Publications dealing with Hybroscale:
- under review -
Publications dealing with the algorithm computing all hybridization networks for multiple binary phylogenetic input trees:
Benjamin Albrecht ,
Computing Hybridization Networks for Multiple Rooted Binary Phylogenetic Trees by Maximum Acyclic Agreement Forests , arXiv:1408.3044, 2014.
Benjamin Albrecht ,
Computing all hybridization networks for multiple binary phylogenetic input trees , BMC Bioinformatics, vol. 16, no. 236, pp. 439-441, 2015.
Publications dealing with an algorithm computing all hybridization networks for two binary phylogenetic input trees:
Celine Scornavacca, Simone Linz,
Benjamin Albrecht ,
A First Step Toward Computing All Hybridization Networks For Two Rooted Binary Phylogenetic Trees , Journal of Computational Biology, vol. 19, no. 11, pp. 1227-1242, 2012.
Benjamin Albrecht , Celine Scornavacca, Alberto Cenci, Daniel H Huson,
Fast computation of minimum hybridization networks , Bioinformatics, vol. 28, no. 2, pp. 191-197, 2011.